找到
1
篇与
损失函数
相关的结果
-
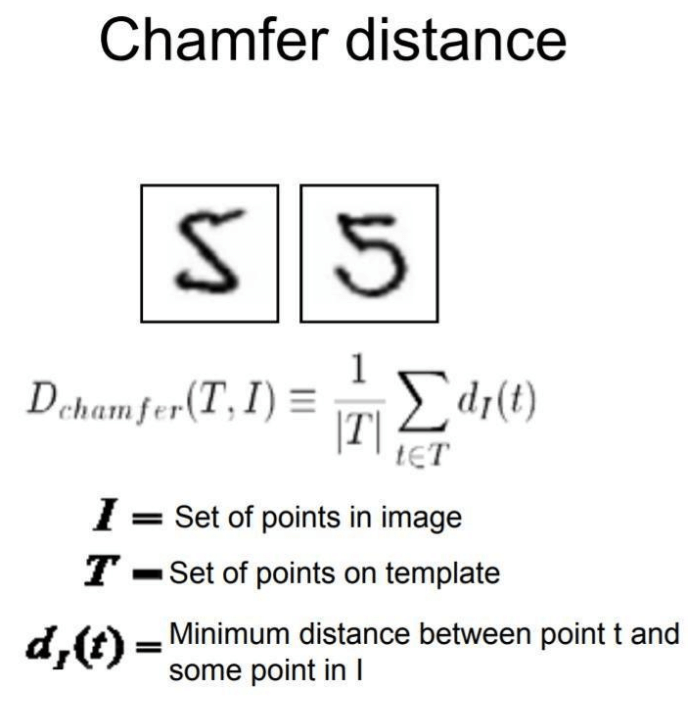
Python 实现 Chamfer 距离：点云相似性度量原理、应用与代码指南 Chamfer 距离（Chamfer Distance, CD）是一种经典的点云相似性度量，广泛用于三维点云完成、配准、模型检索，以及深度学习中的损失函数和评估指标。本文首先介绍 Chamfer 距离的数学定义与变体，包括普通与归一化形式；接着梳理其在点云处理、计算机视觉与机器学习中的典型应用；最后提供两种基于 Python 的实现示例——纯 NumPy 直观版与 SciPy KD-Tree 加速版，帮助开发者快速上手并根据需求优化性能。 1. Chamfer 距离简介 Chamfer 距离（Chamfer Distance, CD）是一种用于评估两组离散点云相似性的“最近邻”度量。它通过计算每个点到另一组点集中最近点的距离之和（或平均），从双向角度量化两点云的重叠与对齐程度。 数学定义（平方欧氏距离） $$ \mathrm{CD}(P, Q) = \sum_{p\in P} \min_{q\in Q} \|p - q\|_2^2 + \sum_{q\in Q} \min_{p\in P} \|q - p\|_2^2 $$ 可选欧氏距离形式 $$ \mathrm{CD}(P, Q) = \sum_{p\in P} \min_{q\in Q} \|p - q\|_2 + \sum_{q\in Q} \min_{p\in P} \|q - p\|_2 $$ 归一化 Chamfer 距离 $$ \mathrm{CD}_{\mathrm{norm}}(P, Q) = \frac{1}{|P|}\sum_{p\in P}\min_{q\in Q}\|p-q\|_2^2 + \frac{1}{|Q|}\sum_{q\in Q}\min_{p\in P}\|q-p\|_2^2 $$ 度量灵活性 可以根据任务需求选择欧氏距离、曼哈顿距离，甚至双曲距离（HyperCD）等。 2. Chamfer 距离的主要应用 三维点云处理 点云完成：作为损失函数与评估指标，量化预测点云与真实点云之间的形状差异； 点云配准：度量不同扫描或模型的对齐质量； 三维模型检索：在数据库中检索形状相似的模型。 计算机视觉 形状匹配与物体检测：基于 Chamfer 系统与定向 Chamfer 距离（OCD）的模板匹配； 图像配准：通过边缘或轮廓对齐多源影像，应用于医学成像与遥感。 机器学习 深度学习损失：点云生成、重建等模型训练的可微距离函数； 评估指标：量化模型输出与真实值之间的几何相似性。 3. 优势与局限 优势局限计算效率高（(O(mn))，可用 KD-Tree 优化）对离群点敏感，易受极端偏差影响灵活性强，支持不同点数对局部密度差异不敏感，可能导致错配对轻微形变与位置偏移具有鲁棒性原始定义非对称，需双向求和或归一化以保证对称性相较于 Earth Mover’s Distance (EMD) 和 Hausdorff 距离，Chamfer 距离在实时或大规模场景下更具实用性，但需针对噪声与密度分布设计相应改进。 4. Chamfer 距离 Python 实现 （1）纯 NumPy 实现（直观版） import numpy as np def chamfer_distance_naive(P: np.ndarray, Q: np.ndarray, squared: bool = True) -> float: """ 计算点云 P, Q 之间的 Chamfer 距离（平方或开方形式）。 P: (m, d), Q: (n, d) """ dist_pq = [] for p in P: dists = np.linalg.norm(Q - p, axis=1) dist_pq.append(dists.min() if not squared else (dists**2).min()) dist_qp = [] for q in Q: dists = np.linalg.norm(P - q, axis=1) dist_qp.append(dists.min() if not squared else (dists**2).min()) return np.sum(dist_pq) + np.sum(dist_qp) # 示例测试 P = np.random.rand(100, 3) Q = np.random.rand(120, 3) print("Chamfer 距离（纯 NumPy，平方）:", chamfer_distance_naive(P, Q, squared=True))（2）KD-Tree 加速实现（高效版） import numpy as np from scipy.spatial import cKDTree def chamfer_distance_kdtree(P: np.ndarray, Q: np.ndarray, normalized: bool = False) -> float: """ 基于 cKDTree 的 Chamfer 距离计算，默认使用平方欧氏距离。 """ tree_P = cKDTree(P) tree_Q = cKDTree(Q) dist_pq, _ = tree_Q.query(P, k=1, n_jobs=-1) dist_qp, _ = tree_P.query(Q, k=1, n_jobs=-1) cd_val = np.sum(dist_pq**2) + np.sum(dist_qp**2) if normalized: cd_val = cd_val / len(P) + cd_val / len(Q) return cd_val # 示例测试 print("Chamfer 距离（KD-Tree，归一化）:", chamfer_distance_kdtree(P, Q, normalized=True))5. 小结与展望 Chamfer 距离以其高效、灵活、鲁棒的特点，已成为点云与形状匹配领域的常用度量。然而，其对离群点与密度变化的敏感性，也催生了多种变体和改进方向： 鲁棒性增强：引入加权机制或密度补偿，降低离群点影响； 全局与局部融合：结合 EMD、谱距离等，提升整体结构一致性； 跨模态扩展：应用于 LiDAR 与 RGB-D 融合、医学影像配准等新场景。 Chamfer 距离图片
