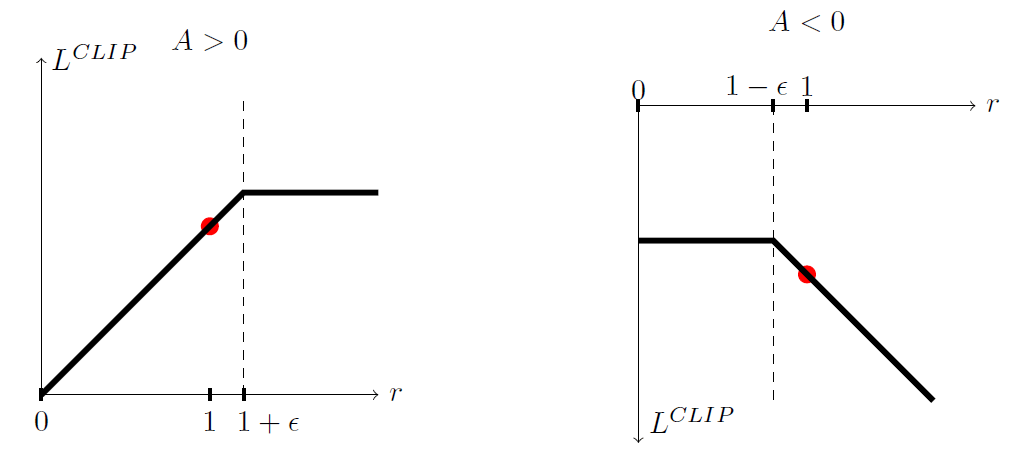找到
1
篇与
样本效率
相关的结果
-
深入浅出阅读OpenAI强化学习经典论文《Proximal Policy Optimization Algorithms》 本文深入浅出地解析了OpenAI强化学习经典论文《Proximal Policy Optimization Algorithms》，从工程视角将PPO算法中的“策略”类比为控制器，帮助非专业背景的读者理解其核心思想。文章详细介绍了PPO的提出背景，指出其在解决传统强化学习算法（如DQN、策略梯度方法和TRPO）的稳定性与复杂性难题中的优势。重点分析了PPO的核心创新——“裁剪”目标函数，通过限制策略更新幅度，在保证训练稳定性的同时简化实现。此外，文章还阐述了PPO的三步工作流程（数据收集、优势计算和优化）及其在连续控制任务和雅达利游戏中的卓越实验效果，最终总结了PPO在样本效率、易用性和性能之间的平衡，奠定了其作为强化学习领域主流算法的地位。 小陶本人不是计算机或者数学专业的，其实学习这些经典算法的时候，一个个公式直接看晕乎了。对于有机械工程或者控制工程背景的我们工科生来说，可以将强化学习中的“策略（Policy）”想象成一个控制器，它的目标是学会如何操作一个复杂的系统（比如机器人或游戏角色），以获得最大的累计奖励（比如最快到达终点或获得最高分）。PPO算法就是一种设计这个“控制器”的优秀方法。本文结合论文的原文并且适当使用AI进行整理。如果明显的错误，欢迎指出交流。 论文原文：Proximal Policy Optimization Algorithms - arXiv:1707.06347 PPO的提出背景：为什么我们需要PPO？ 在PPO被提出之前，主流的强化学习算法主要有三类，但它们都各有短处： （1）深度Q学习 (DQN): 这类算法在处理像雅达利（Atari）游戏这样拥有离散动作（比如上、下、左、右）的环境中表现优异 。但它很难被应用到动作是连续的场景中（比如控制机器人关节的角度） ，并且在一些简单问题上有时也表现不佳 。 （2）“香草”策略梯度 (Vanilla Policy Gradient, PG): 这类算法可以直接优化策略，能处理连续动作问题。但它有一个很大的缺点：训练过程非常不稳定，对参数敏感。想象一下你在调试一个控制器参数，稍微调大一点，系统就可能直接崩溃。PG算法就有类似的问题，它在更新策略时步子迈得太大，很容易导致策略“学废了”，性能急剧下降 。 （3）信任区域策略优化 (Trust Region Policy Optimization, TRPO): TRPO是为了解决PG算法不稳定的问题而设计的。它的核心思想是：在更新策略时，给新策略加一个“信任区域”的约束，确保新策略不会和旧策略偏离太远，从而保证了学习过程的稳定。TRPO效果很好，但它的算法实现异常复杂 ，需要用到二阶优化，并且与一些常见的网络结构（如参数共享、Dropout）不兼容 。 PPO的目标就是： 创造一种新算法，既能拥有TRPO的稳定性和可靠性能，又能像PG算法一样简单，只用一阶优化（也就是我们常用的梯度下降/上升），更容易实现和应用 。 PPO的核心思想：神奇的“裁剪”目标函数 PPO的精髓在于它设计了一个巧妙的“代理”目标函数（Surrogate Objective Function）。在更新策略时，我们优化的不是真实的回报，而是这个代理目标，通过优化它来间接提升策略。 要理解这个目标函数，我们先来看一个关键的比率：概率比率 (Probability Ratio)。 $$ r _ { t } ( \theta ) = \frac { \pi _ { \theta } ( a _ { t } | s _ { t } ) } { \pi _ { \theta _ { o l d } } ( a _ { t } | s _ { t } ) } $$ 分子是新策略在状态St下采取动作at的概率； 分母是旧策略在同样状态下采取同样动作的概率； 这个比值 $r _ { t }$ 度量了新旧策略的差异。如果 $r_t>1$，说明新策略更倾向于采取这个动作；如果$ r_t<1$，则说明新策略更不倾向于采取这个动作 。 传统的策略梯度算法的目标函数可以简化为 : $$ L ^ { C P I } ( \theta ) = r _ { t } ( \theta ) \hat { A } _ { t } $$其中 $ \hat { A } _ { t } $ 是优势函数 (Advantage Function)，它衡量了在状态$ s _ { t } $采取动作$ a _ { t } $究竟有多好。如果 $ \hat { A } _ { t } $ \>0，说明这个动作比平均水平要好；反之则不好。 所以，优化的目标就是：如果一个动作是“好”的，就增大它的概率，如果一个动作是“坏”的，就减小它的概率。 那么，问题来了，如果毫无限制地增大$r _ { t }$，就可能导致策略更新步子太大，这就是PG算法不稳定的根源 。PPO的解决方案是裁剪 (Clipping)。 PPO的目标函数如下： $$ L ^ { C L I P } ( \theta ) = \hat { \mathbb { E } } _ { t } \left[ \operatorname* { m i n } \left( r _ { t } ( \theta ) \hat { A } _ { t } , \operatorname { c l i p } ( r _ { t } ( \theta ) , 1 - \epsilon , 1 + \epsilon ) \hat { A } _ { t } \right) \right] $$这里的$\epsilon$是一个超参数，通常取0.2左右 。这个公式看起来复杂，但思想很直观，我们可以把它看作一个“带有限位器的激励系统”（如下图所示）： 带有限位器的激励系统图片 当动作是“好”的 $( \hat { A } _ { t } > 0 )$: 目标函数变为$ \operatorname* { m i n } ( r _ { t } \hat { A } _ { t } , ( 1 + \epsilon ) \hat { A } _ { t } ) $ 我们希望增大$r _ { t }$来获得更大的回报，但函数外部的 min 操作给这个回报设置了一个上限。一旦$r _ { t }$超过 1+ϵ，回报就不会再增加了。 这就好比： 你做得好，就给你奖励，但奖励有个上限，防止你因为一次超常发挥就变得过于激进，从而保证了稳定性。 当动作是“坏”的$( \hat { A } _ { t } < 0 )$: 目标函数变为${ m i n } ( r _ { t } \hat { A } _ { t } , ( 1 - \epsilon ) \hat { A } _ { t } )$ 我们希望减小$r _ { t }$，但如果优化的过程中，算法错误地增大了$r _ { t }$（比如超过了 1+ϵ），$r _ { t } \hat { A } _ { t }$这一项会变成一个很大的负数，给予一个严厉的惩罚。 clip 的作用是，当$r _ { t }$减小到1−ϵ 以下时，目标函数的值不再变化 。这同样限制了单步更新的幅度。 这就好比： 你做得不好，就要接受惩罚。这个机制确保了你不会因为想逃避惩罚而做出过于保守或奇怪的动作，同时也对错误方向的更新给予重罚。 通过上述的约束，这个“裁剪”的目标函数通过限制策略更新的幅度，巧妙地将TRPO的“信任区域”思想用一种更简单的方式实现了，使得算法既稳定又易于实现 。 PPO如何Work：三步走的循环 PPO作为一个“演员-评论家（Actor-Critic）”风格的算法，其工作流程非常清晰 ： 第一步：数据收集 首先，我们有N个并行的“演员”（Actor），它们使用当前的策略$\pi _ { \theta _ { o l d } }$与环境互动，各自收集T个时间步的数据（状态、动作、奖励等） 。 第二步：优势计算 利用收集到的数据，计算每个时间步的优势函数估计值$( \hat { A } _ { t } $。这通常通过一种叫做“广义优势估计 (GAE)”的技术来完成 。 第三步：优化 将收集到的 NT 条数据作为一个批次（batch），用这个批次的数据来优化上面提到的 目标函数 $L ^ { C L I P } $。 关键点：PPO会用同一批数据，通过随机梯度上升（如Adam优化器）进行多轮（K epochs）的优化 。这极大地提高了数据的利用率，也是它相比于PG算法数据效率更高的原因。因为有“裁剪”机制的保护，多轮更新也不会导致策略崩溃 。 这三步完成后，更新策略参数，然后无限循环下去，策略就会变得越来越好。 PPO实验效果 它真的好用吗？答案是肯定的。论文通过大量的实验证明了PPO的有效性。 在连续控制任务上（如模拟机器人行走）:论文首先验证了“裁剪”目标函数的有效性。不带任何限制的版本性能很差，甚至比随机策略还糟糕，而带有裁剪的版本（ϵ=0.2）在所有变体中得分最高 。在与其他主流算法（如TRPO, A2C）的对比中，PPO在绝大多数任务上都取得了最好的性能，学习速度更快，最终表现也更优越 (具体可见论文Figure 3的曲线图)。 PPO的有效性图片 在雅达利游戏上（离散控制任务），PPO同样表现出色。论文在49个游戏上对比了PPO, A2C和ACER。如果衡量“学习速度”（整个训练过程的平均分），PPO在30个游戏中胜出，遥遥领先 。如果衡量“最终性能”（训练最后100个回合的平均分），PPO的表现也极具竞争力，虽然胜出游戏数量少于ACER，但考虑到PPO的实现简单得多，这个结果已经非常惊人了 。 雅达利游戏上（离散控制任务）图片 论文总结 PPO通过引入一个创新的裁剪代理目标函数，成功地实现了与复杂算法TRPO相媲美的稳定性和性能，同时保持了代码实现的简洁性 。它解决了传统策略梯度方法更新步长难以确定、容易崩溃的问题，也避免了信任区域方法的复杂计算。总的来说，PPO在样本效率、实现简单性和性能表现之间找到了一个绝佳的平衡点 ，这也是它至今仍然是强化学习研究和应用领域最常用和最受欢迎的算法之一的原因。
