欢迎来到小陶的技术博客。如果你和我一样,是一名刚刚踏入三维点云处理世界的新手,你一定听说过 PointNet 和 PointNet++ 这两个大名鼎鼎的模型。它们就像是3D视觉领域的“开山鼻祖”,理解了它们,学习之路会顺畅很多。
今天,我也是根据自己看的一些别的博客资料以及B站视频,梳理这两个模型的“来龙去脉”和核心思想。
为什么要有点云模型?传统方法不行吗?
深入了解PointNet之前,先问一个问题:我们熟悉的二维图片处理方法(比如CNN,卷积神经网络)为什么不能直接用在三维点云上?
想象一下,一张图片就像一个整齐的棋盘,每个像素都有自己固定的位置。CNN的“卷积核”就像一个小窗口,在棋盘上规律地滑来滑去,提取特征。但点云完全不同,它就像一把随意撒在空中的沙子。它有两大特性,让CNN直接“水土不服”:
- 无序性 (Unordered): 一堆点,你先看A点再看B点,和我先看B点再看A点,描述的应该是同一个物体。点的顺序不应该影响最终结果。但对于传统神经网络,输入顺序变了,结果可能就天差地别。
- 空间结构性 (Sparsity & Irregularity): 点云不像像素那样均匀分布,它可能在某些地方密集(比如物体的棱角),在某些地方稀疏(比如一个平面)。你没法像CNN那样用一个固定大小的窗口去“滑动”。
为了解决这两个核心痛点,PointNet应运而生。
PointNet:简单粗暴的“大力出奇迹”
PointNet是第一个直接处理原始点云的深度学习模型,它的想法堪称“天才般的简单”。
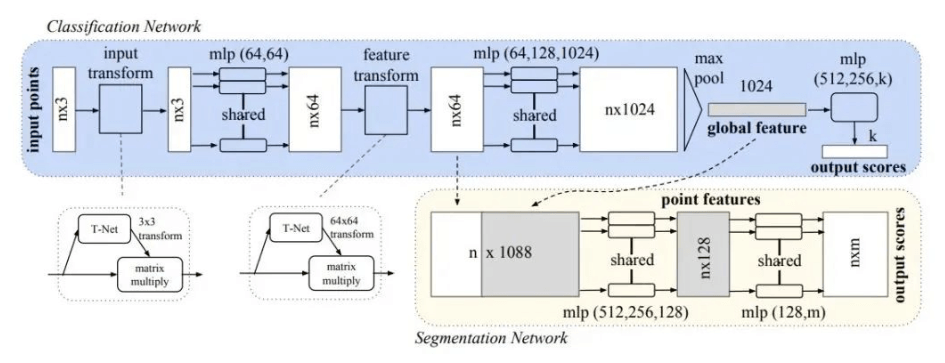
核心思想:如何解决“无序性”?
PointNet的作者想:我需要找到一种方法,无论点的顺序怎么打乱,我最后得到的特征都是一样的。这种特性在数学上叫做“对称函数” (Symmetric Function)。
常见的对称函数有哪些?
- 求和 (Summation):
a+b+c和c+b+a的结果是一样的。 - 求平均 (Average):
(a+b+c)/3和(c+b+a)/3的结果是一样的。 - 求最大值 (Max-Pooling):
max(a, b, c)和max(c, b, a)的结果是一样的。
PointNet最终选择了 Max-Pooling(最大池化) 作为它的核心对称函数。
PointNet工作流程(三步走):
独立特征提取:
- 输入是一堆点的坐标(一个大小为
N x 3的矩阵,N是点的数量,3是XYZ坐标)。 - PointNet对 每一个点 单独进行特征学习,把它从3维映射到更高维度的空间(比如1024维)。你可以把它想象成给每个点“画像”,让它的信息更丰富。这一步是通过几个共享参数的多层感知机(MLP)完成的。
- 输入是一堆点的坐标(一个大小为
全局特征聚合(关键一步):
- 现在我们有N个1024维的特征向量了。
- PointNet在这些特征向量的 每一个维度上 做一次Max-Pooling。也就是说,在第一个维度上,从N个点中选出最大值;在第二个维度上,也选出最大值……以此类推。
- 做完之后,N个点的特征就被“压”成了一个1024维的 全局特征向量。这个向量代表了整个点云的“样子”。因为Max-Pooling是无序的,所以无论输入点的顺序如何,这个全局特征都是不变的!
输出结果:
- 最后,用这个全局特征向量去做具体的任务,比如接一个分类器判断这个点云是什么物体(桌子?椅子?),或者做一个分割器判断每个点属于物体的哪个部分。
# PointNet用于分类任务的伪代码
function pointnet_classification(point_cloud):
# point_cloud 是一组N个点 {p1, p2, ..., pN}
# 1. 对每个点独立应用MLP,提取高维特征
point_features = []
for point in point_cloud:
# 比如把 (x,y,z) 变成一个1024维的特征
feature = MLP(point)
point_features.append(feature)
# 2. 使用对称函数(Max-Pooling)聚合所有点的特征
# 这是保证顺序不变性的核心!
# 从 [N, 1024] 的特征矩阵,池化成 [1, 1024] 的全局特征
global_feature = max_pool(point_features)
# 3. 使用最后的MLP进行分类
prediction_scores = MLP(global_feature)
return prediction_scoresPointNet虽然开创了历史,但它的方法太“粗暴”了。它通过Max-Pooling把所有点的信息都揉成一团,形成一个全局特征。这导致它 无法感知局部细节。
打个比方,PointNet能认出这是一辆车,但它很难分清车轮和车灯的区别,因为它把所有点的特征“一视同仁”地混合了,丢失了点与点之间的邻里关系和局部几何结构。
PointNet++:从“全局”到“局部”的精细化升级
为了解决PointNet丢失局部结构的问题,PointNet++被提了出来。它的核心思想非常像我们熟悉的CNN,那就是——层次化特征提取 (Hierarchical Feature Learning)。
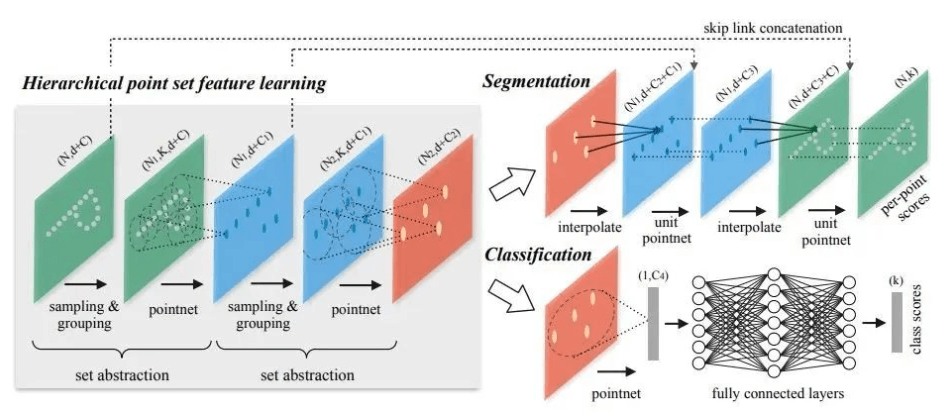
核心思想:先局部,再整体
如果说PointNet是“一口吃成个胖子”,那PointNet++就是“细嚼慢咽”。它不再直接对所有点进行粗暴的全局池化,而是:
- 分片 (Partition): 在点云中选择几个“中心点”。
- 分组 (Grouping): 以每个中心点为核心,在周围画一个“圈”(比如一个球形半径内),把邻近的点组织成一个小局部区域。
- 小PointNet提取局部特征: 对每一个小局部区域,使用一个迷你的PointNet来提取这个区域的局部特征。
- 迭代升级: 不断重复以上过程。上一层提取的局部特征,会成为下一层分组和提取的输入。这样一来,网络就能从非常小的局部细节(比如桌子腿的棱角),逐渐学习到更大范围的特征(整个桌子腿),最后再到全局特征(整张桌子)。
这个核心组件,PointNet++称之为 集合抽象层 (Set Abstraction Layer)。
一个Set Abstraction Layer的伪代码:
# PointNet++ 中一个 Set Abstraction 层的伪代码
function set_abstraction_layer(points, features):
# points是输入的点集,features是这些点对应的特征
# 1. 采样层:用最远点采样(FPS)选出一些中心点
centroids = farthest_point_sampling(points)
# 2. 分组层:为每个中心点,找到它的邻居点
groups = []
for c in centroids:
# 比如在半径r内找邻居 (Ball Query)
neighbors = find_neighbors_in_radius(c, points, radius)
groups.append(neighbors)
# 3. PointNet层:对每个组用一个“迷你PointNet”来提取局部特征
new_features = []
for group in groups:
# 注意:在送入迷你PointNet前,会先将邻居点坐标归一化到局部坐标系
local_feature = mini_pointnet_module(group)
new_features.append(local_feature)
# 输出:新的点(中心点)和它们对应的更高级的特征
return centroids, new_features通过堆叠多个这样的set_abstraction_layer,PointNet++就能像CNN一样,一层层地扩大感受野,从点到线,从线到面,最终理解整个三维物体的复杂结构。
如果还没理解,我们来做一个最后的比喻:
- PointNet: 就像全国海选。所有选手(点)都来到一个大舞台上,评委(Max-Pooling)只看一眼,选出最亮眼的那一个(最大特征值)来代表所有人。这个方法简单高效,能快速得到一个总体印象,但忽略了选手们在各自地区(局部)的特色。
- PointNet++: 就像分级选举。先在每个村里选出村代表(第一层局部特征),然后村代表们再开会选出镇代表(第二层更大范围的特征),镇代表再选出县代表……最后选出国家主席(最终的全局特征)。这个过程更复杂,但能充分保留从基层到高层的各级信息,对情况的把握更精细。
| 特性 | PointNet | PointNet++ |
|---|---|---|
| 核心思想 | 对称函数(Max-Pooling)处理无序性 | 层次化特征提取 |
| 结构感知 | 仅有全局特征,无局部结构信息 | 有局部结构信息,从局部到全局 |
| 处理方式 | 一步到位,简单粗暴 | 逐层抽象,精细复杂 |
| 适用场景 | 简单的分类任务,对细节要求不高的场景 | 分割、复杂场景理解等需要局部信息的任务 |
| 比喻 | 全国海选 | 分级选举 |
写在最后
PointNet和PointNet++是3D点云深度学习的基石。虽然现在已经有了更多更复杂的模型,但它们的思想——如何解决无序性、如何学习局部和全局特征——依然在影响着后续的研究。
对于初学者来说,不必急于深究代码的每一个细节,最重要的是理解其背后的思想。
