点云数据标准化（归一化）：常用方法及可视化对比的Python实现

本文详细解析三维点云数据标准化的核心方法，包括最小-最大缩放、Z-Score标准化和单位球归一化，对比其原理、优缺点及适用场景。通过Python代码实战演示各方法的实现与反归一化操作，并基于PyVista可视化对比不同标准化效果。文章提供完整的代码示例和可视化方案，助力开发者在自动驾驶、三维重建等场景中优化点云预处理流程，提升机器学习模型性能。

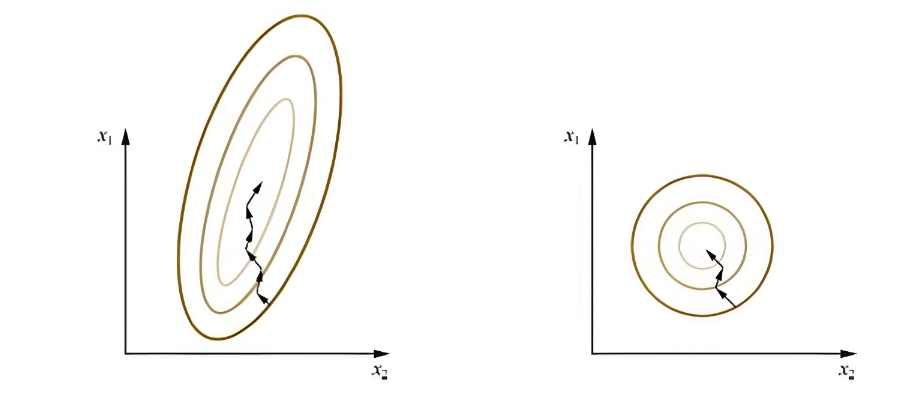
标准化作用

三维点云作为一种重要的几何数据表示形式，广泛应用于自动驾驶、机器人、文物数字化等领域. 然而，由不同设备或在不同环境下采集的点云数据，往往在尺度、平移和方向上存在差异，这会严重影响后续的点云处理与分析任务的性能. 例如，在机器学习中，如果特征的尺度差异过大，可能导致模型训练不稳定、收敛速度慢，甚至影响最终的预测精度.

点云标准化（Normalization）是一种关键的预处理技术，旨在将点云数据转换到一个统一的尺度或范围，消除原始数据中的差异，使得不同的点云可以在相同的基准下进行比较和分析. 通过标准化，我们可以提高算法的鲁棒性、加快模型的收敛速度，并提升整体的性能.

常见方法及对比

方法名称	原理	优点	缺点	典型应用场景
最小-最大缩放	将数据线性缩放到或[-1, 1]的指定范围	实现简单，保留原始数据的分布形状	对异常值敏感	数据范围有明确边界，且对尺度不敏感的场景
Z-Score标准化	将数据转换为均值为0，标准差为1的标准正态分布	对异常值不敏感，适用于大多数机器学习算法	没有固定的输出范围	大多数情况，尤其是在使用基于距离或假设数据服从正态分布的算法时
归一化到单位球	将点云平移到原点，并缩放到半径为1的球体内	使点云在平移和尺度上保持一致，便于形状比较和分析	可能会改变原始点云中点与点之间的相对距离比例	形状分析、形状识别等需要统一尺度和中心的应用

最小-最大缩放 (Min-Max Scaling)

（1）原理

最小-最大缩放通过以下公式将点云的每个维度缩放到的范围内 :

x_normalized = (x - min(x)) / (max(x) - min(x))

其中，x是原始的坐标值，min(x)和max(x)分别是该维度上的最小值和最大值。

（2）Python代码实现

import numpy as np

def min_max_normalize(points, feature_range=(0, 1)):
    """
    对点云数据进行最小-最大归一化，支持自定义范围（如[0,1]或[-1,1]）。

    Args:
        points (np.ndarray): (N, 3) 的NumPy数组，表示N个点的x, y, z坐标。
        feature_range (tuple): 目标范围，默认为(0, 1)。

    Returns:
        tuple: 包含归一化后的点云、每个维度的最小值、最大值和目标范围。
    """
    min_coords = np.min(points, axis=0)
    max_coords = np.max(points, axis=0)
    data_range = max_coords - min_coords
    data_range[data_range == 0] = 1e-8  # 处理全零维度
    
    range_min, range_max = feature_range
    normalized_points = (points - min_coords) / data_range  # 缩放到[0,1]
    normalized_points = normalized_points * (range_max - range_min) + range_min  # 缩放到目标范围
    
    return normalized_points, min_coords, max_coords, feature_range

（3）反归一化Python实现

def min_max_denormalize(normalized_points, min_coords, max_coords, feature_range=(0, 1)):
    """
    反归一化时需传入原始范围参数。
    """
    range_min, range_max = feature_range
    data_range = max_coords - min_coords
    # 先将数据从目标范围映射回[0,1]
    normalized_in_01 = (normalized_points - range_min) / (range_max - range_min + 1e-8)
    denormalized_points = normalized_in_01 * data_range + min_coords
    return denormalized_points

Z-Score标准化 (Z-Score Standardization)

（1）原理

Z-Score标准化通过以下公式将点云的每个维度转换为均值为0，标准差为1的分布 :

x_standardized = (x - mean(x)) / std(x)

其中，mean(x)是该维度上的均值，std(x)是该维度上的标准差。

（2）Python代码实现

def z_score_standardize(points):
    """
    对点云数据进行Z-Score标准化。

    Args:
        points (np.ndarray): (N, 3) 的NumPy数组，表示N个点的x, y, z坐标。

    Returns:
        tuple: 包含标准化后的点云、每个维度的均值和标准差。
    """
    mean_coords = np.mean(points, axis=0)
    std_coords = np.std(points, axis=0)
    standardized_points = (points - mean_coords) / (std_coords + 1e-8) # 添加一个小的epsilon防止除以零
    return standardized_points, mean_coords, std_coords

（3）反归一化Python实现

def z_score_denormalize(standardized_points, mean_coords, std_coords):
    """
    对Z-Score标准化后的点云进行反归一化。

    Args:
        standardized_points (np.ndarray): 标准化后的点云数据。
        mean_coords (np.ndarray): 原始点云每个维度的均值。
        std_coords (np.ndarray): 原始点云每个维度的标准差。

    Returns:
        np.ndarray: 反归一化后的点云数据。
    """
    denormalized_points = standardized_points * std_coords + mean_coords
    return denormalized_points

归一化到单位球 (Normalization to Unit Sphere)

（1）原理

归一化到单位球首先将点云的中心平移到坐标原点，然后缩放整个点云，使得所有点到原点的最大距离为1.

中心化: 计算点云的质心，并将每个点的坐标减去质心。
缩放: 计算中心化后点云中所有点到原点的最大距离，并将每个点的坐标除以该最大距离。

（2）python代码实现

def normalize_to_unit_sphere(points):
    """
    将点云数据归一化到单位球。

    Args:
        points (np.ndarray): (N, 3) 的NumPy数组，表示N个点的x, y, z坐标。

    Returns:
        tuple: 包含归一化后的点云、原始点云的质心和最大距离。
    """
    centroid = np.mean(points, axis=0)
    centered_points = points - centroid
    max_distance = np.max(np.linalg.norm(centered_points, axis=1))
    normalized_points = centered_points / (max_distance + 1e-8) # 添加一个小的epsilon防止除以零
    return normalized_points, centroid, max_distance

（3）反归一化Python实现

def denormalize_unit_sphere(normalized_points, centroid, max_distance):
    """
    对归一化到单位球的点云进行反归一化。

    Args:
        normalized_points (np.ndarray): 归一化后的点云数据。
        centroid (np.ndarray): 原始点云的质心。
        max_distance (float): 原始点云到质心的最大距离。

    Returns:
        np.ndarray: 反归一化后的点云数据。
    """
    denormalized_points = normalized_points * max_distance + centroid
    return denormalized_points

归一化与可视化对比

下面我基于pyvista 进行可视化。

import numpy as np
import pyvista as pv

# 加载点云数据
def load_point_cloud(file_path):
    """从文本文件加载点云数据。"""
    try:
        points = np.loadtxt(file_path)
        return points
    except FileNotFoundError:
        print(f"错误：文件 {file_path} 未找到。")
        return None
    except Exception as e:
        print(f"加载文件时发生错误：{e}")
        return None

def min_max_normalize(points, feature_range=(0, 1)):
    """
    对点云数据进行最小-最大归一化，支持自定义范围（如[0,1]或[-1,1]）。

    Args:
        points (np.ndarray): (N, 3) 的NumPy数组，表示N个点的x, y, z坐标。
        feature_range (tuple): 目标范围，默认为(0, 1)。

    Returns:
        tuple: 包含归一化后的点云、每个维度的最小值、最大值和目标范围。
    """
    min_coords = np.min(points, axis=0)
    max_coords = np.max(points, axis=0)
    data_range = max_coords - min_coords
    data_range[data_range == 0] = 1e-8  # 处理全零维度
    
    range_min, range_max = feature_range
    normalized_points = (points - min_coords) / data_range  # 缩放到[0,1]
    normalized_points = normalized_points * (range_max - range_min) + range_min  # 缩放到目标范围
    
    return normalized_points, min_coords, max_coords, feature_range
def z_score_standardize(points):
    mean_coords = np.mean(points, axis=0)
    std_coords = np.std(points, axis=0)
    standardized_points = (points - mean_coords) / (std_coords + 1e-8)
    return standardized_points, mean_coords, std_coords

def normalize_to_unit_sphere(points):
    centroid = np.mean(points, axis=0)
    centered_points = points - centroid
    max_distance = np.max(np.linalg.norm(centered_points, axis=1))
    normalized_points = centered_points / (max_distance + 1e-8)
    return normalized_points, centroid, max_distance

if __name__ == "__main__":
    file_path = "point_cloud.txt"  # 点云文件路径
    original_points = load_point_cloud(file_path)

    if original_points is not None:
        # 应用最小-最大归一化
        min_max_normalized_points, _, _ = min_max_normalize(original_points.copy())

        # 应用Z-Score标准化
        z_score_normalized_points, _, _ = z_score_standardize(original_points.copy())

        # 应用归一化到单位球
        unit_sphere_normalized_points, _, _ = normalize_to_unit_sphere(original_points.copy())

        # 可视化
        plotter = pv.Plotter(shape=(2, 2))

        # 原始点云
        plotter.subplot(0, 0)
        cloud = pv.PolyData(original_points)
        plotter.add_mesh(cloud, color="blue", point_size=3, render_points_as_spheres=True)
        plotter.add_text("Original Point Cloud", position="upper_left", color="black")

        # 最小-最大归一化后的点云
        plotter.subplot(0, 1)
        normalized_cloud_minmax = pv.PolyData(min_max_normalized_points)
        plotter.add_mesh(normalized_cloud_minmax, color="red", point_size=3, render_points_as_spheres=True)
        plotter.add_text("Min-Max Normalized", position="upper_left", color="black")

        # Z-Score标准化后的点云
        plotter.subplot(1, 0)
        normalized_cloud_zscore = pv.PolyData(z_score_normalized_points)
        plotter.add_mesh(normalized_cloud_zscore, color="green", point_size=3, render_points_as_spheres=True)
        plotter.add_text("Z-Score Standardized", position="upper_left", color="black")

        # 归一化到单位球后的点云
        plotter.subplot(1, 1)
        normalized_cloud_unit_sphere = pv.PolyData(unit_sphere_normalized_points)
        plotter.add_mesh(normalized_cloud_unit_sphere, color="purple", point_size=3, render_points_as_spheres=True)
        plotter.add_text("Normalized to Unit Sphere", position="upper_left", color="black")

        plotter.show()

将代码中的 point_cloud.txt 替换为包含您的点云数据的实际文件路径。

运行此脚本将显示一个包含四个子图的窗口，分别展示了原始点云和三种标准化后的点云，它们以不同的颜色区分。

点云标准化对比1

点云标准化对比2

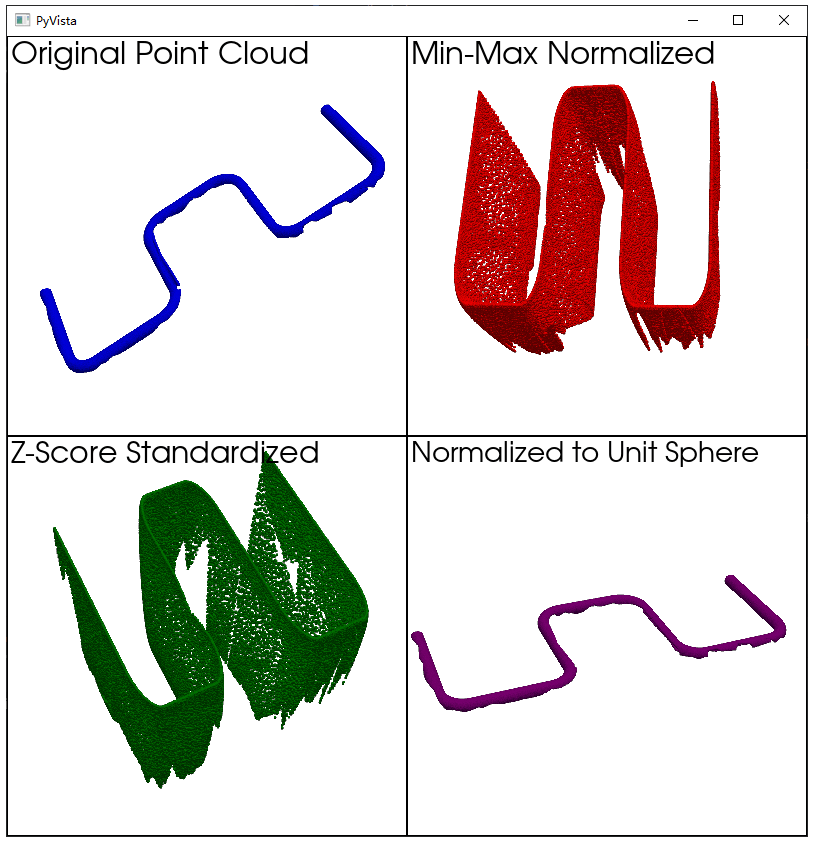
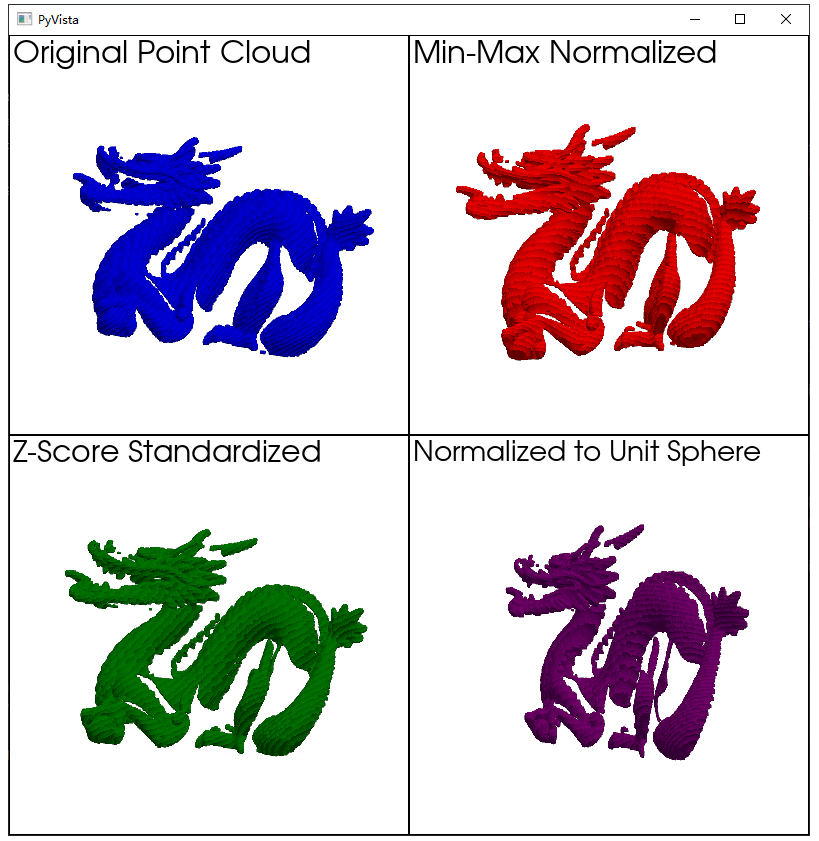
从上面两个点云可以看出，在进行归一化操作之前需要仔细观察一下哪种归一化方法适合自己正在处理的模型，有时候不一定通用。